Sigmoid
介绍
Sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
公式
$$ \sigma(x)= \frac{1}{1+e^{-x}} $$
导数
$$ \sigma'(x)=\frac{e^{-x}}{(1+e^{-x})^2}=\sigma(x)(1-\sigma(x)) $$
图像
Sigmoid函数
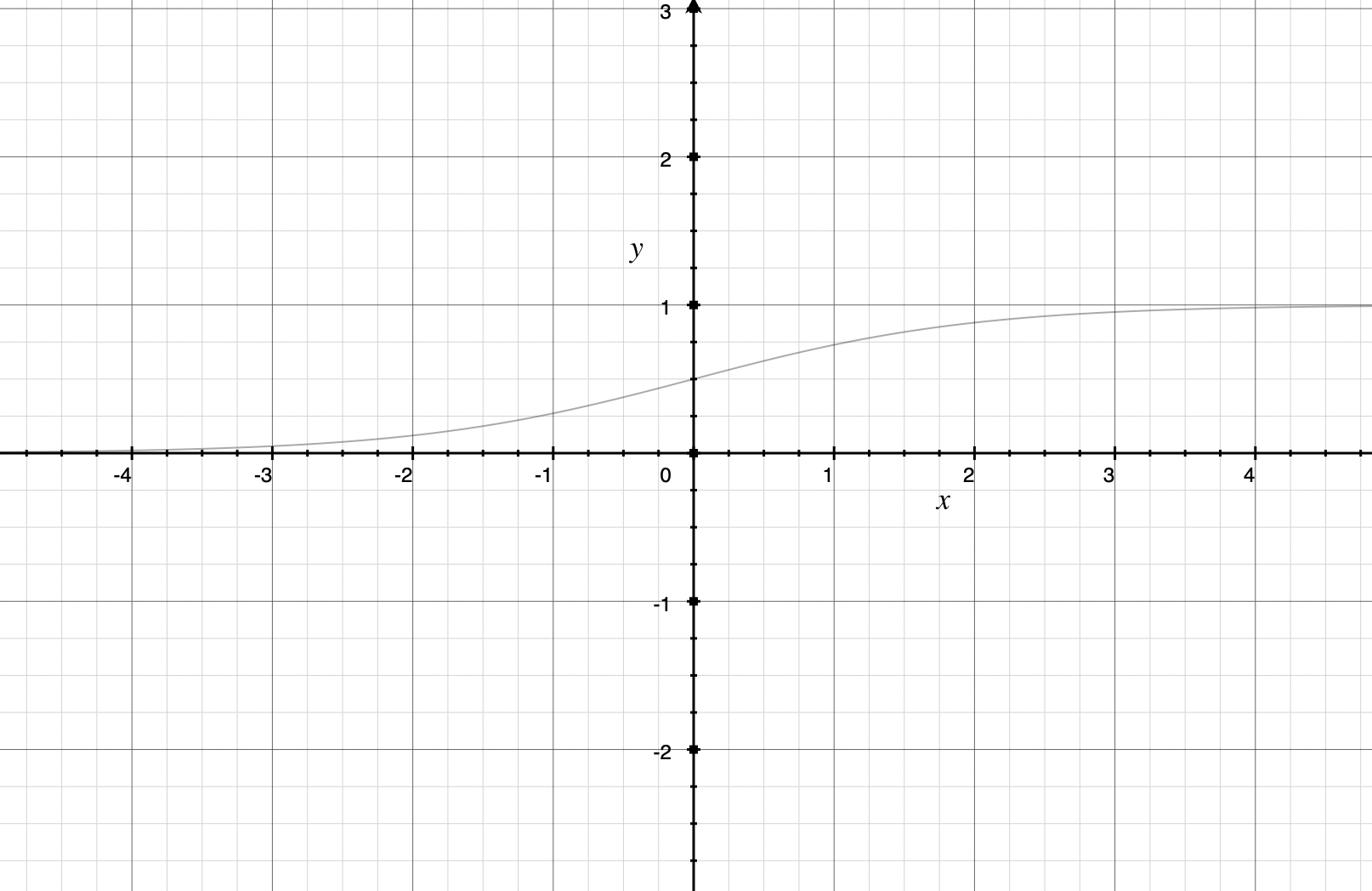
Sigmoid函数导数
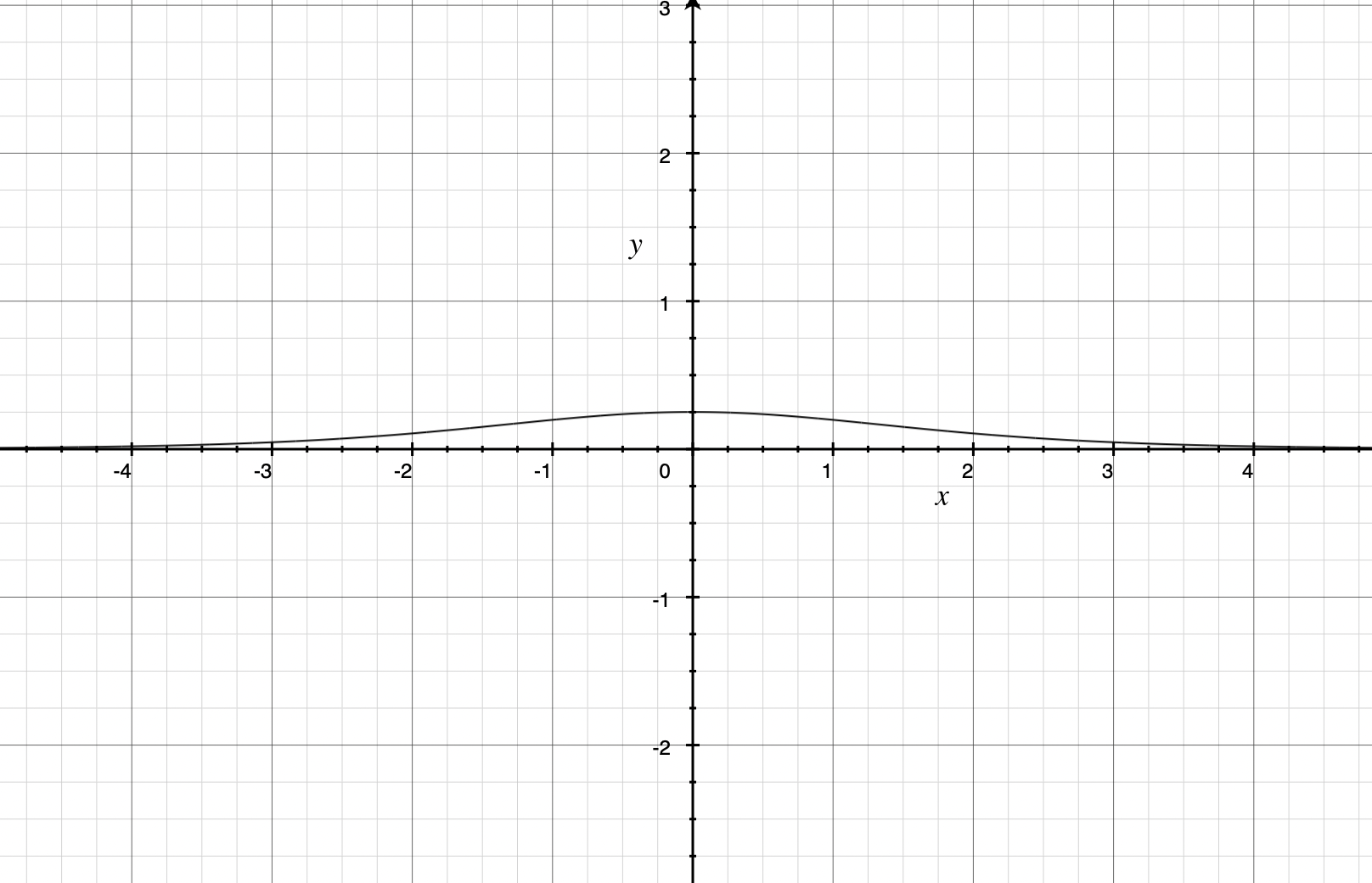
Python代码实现
import numpy as np
def sigmoid(Z):
""" sigmoid函数计算 """
return 1/(1+np.exp(-Z))
def sigmoid_derivatice(Z):
""" sigmoid函数导数计算 """
return sigmoid(Z)*(1-sigmoid(Z))
Tanh
介绍
双曲正切函数(hyperbolic tangent function)是双曲函数的一种。双曲正切函数在数学语言上一般写作tanh,也可简写成th。
公式
$$ tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} $$
导数
$$ tanh'(x)=1-tanh^2(x) $$
图像
Tanh函数
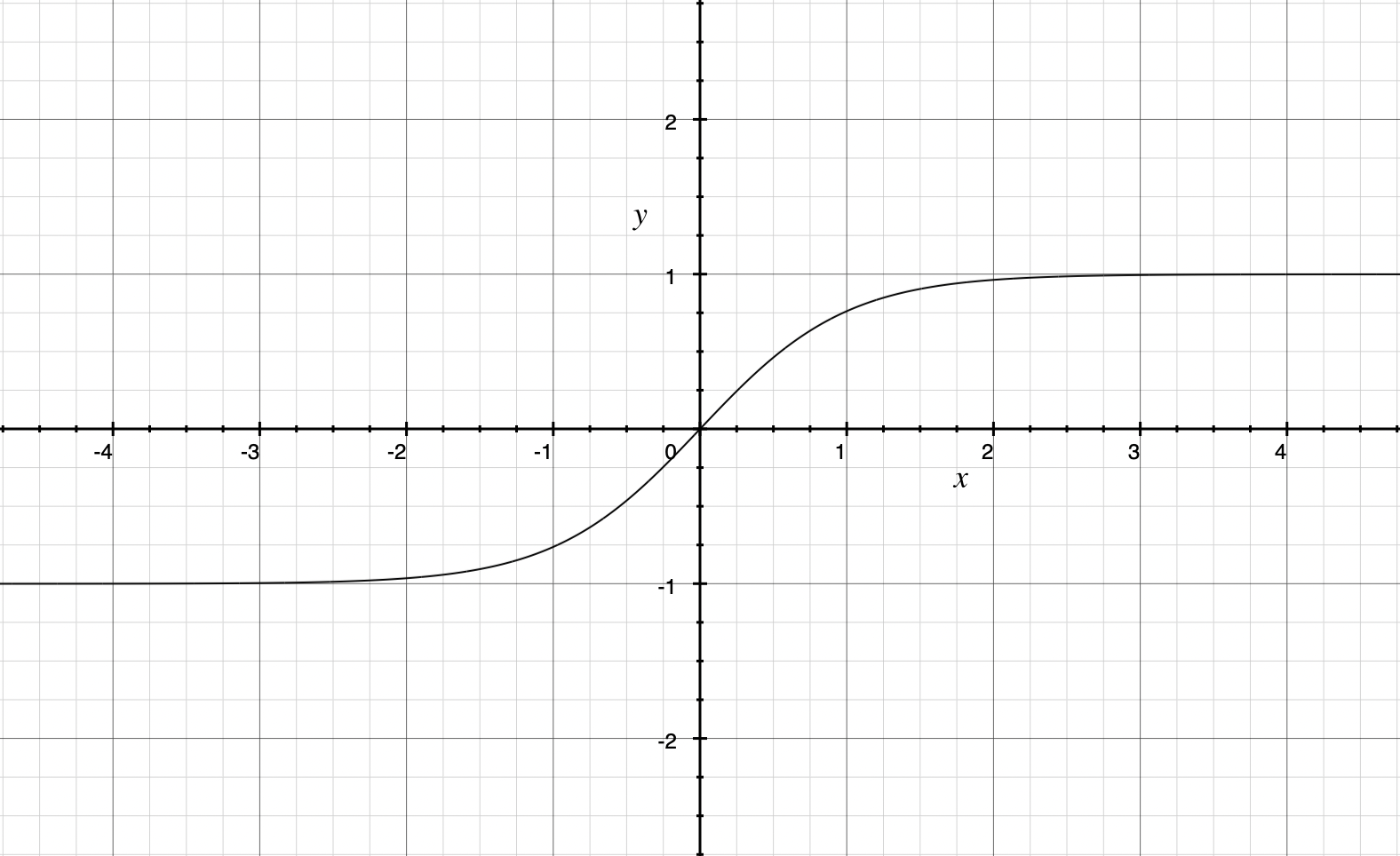
Tanh函数导数
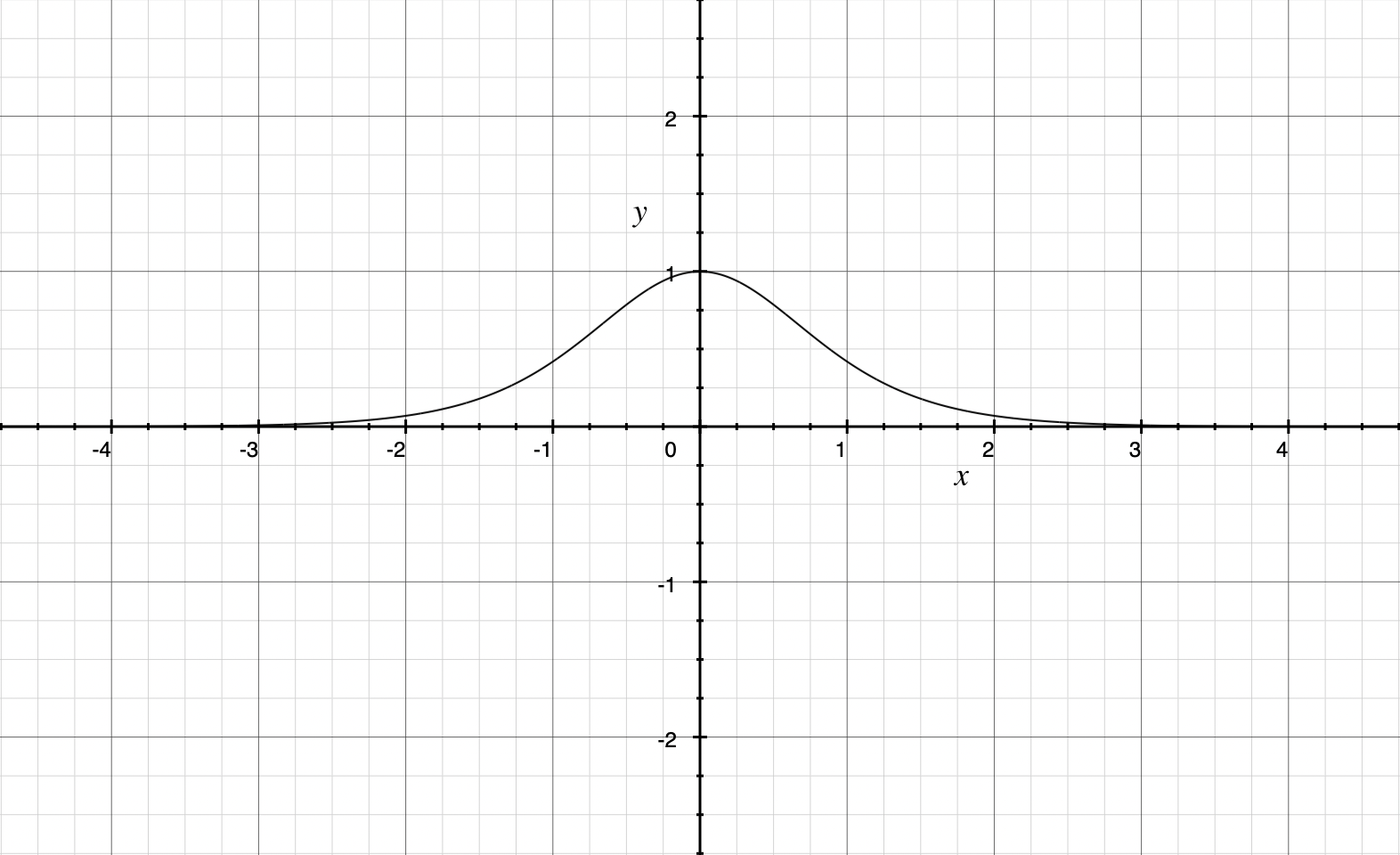
Python代码实现
import numpy as np
def tanh(Z):
""" tanh函数计算 """
return (np.exp(Z)-np.exp(-Z))/(np.exp(Z)+np.exp(-Z))
def tanh_derivative(Z):
""" tanh函数导数计算 """
return 1-tanh(Z)**2
ReLU
介绍
线性整流函数(Rectified Linear Unit, ReLU),又称修正线性单元,是一种人工神经网络中常用的激活函数,通常指代以斜坡函数及其变种为代表的非线性函数。
公式
$$ f(x)=max(0, x) $$
导数
$$ f'(x)=\begin{cases} 0 \quad x< 0 \\ 1 \quad x>0\end{cases} $$
图像
ReLU函数
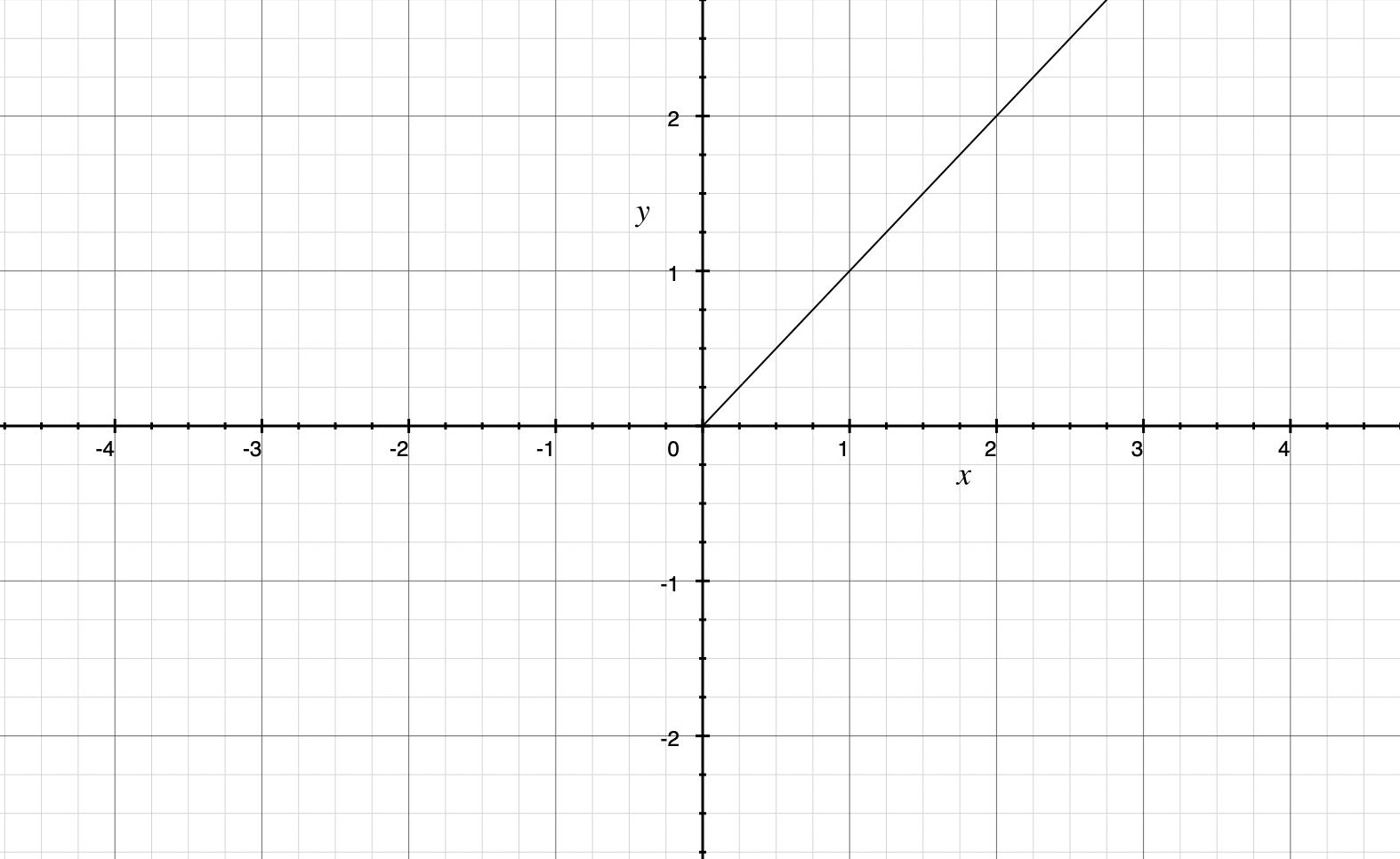
ReLU函数导数
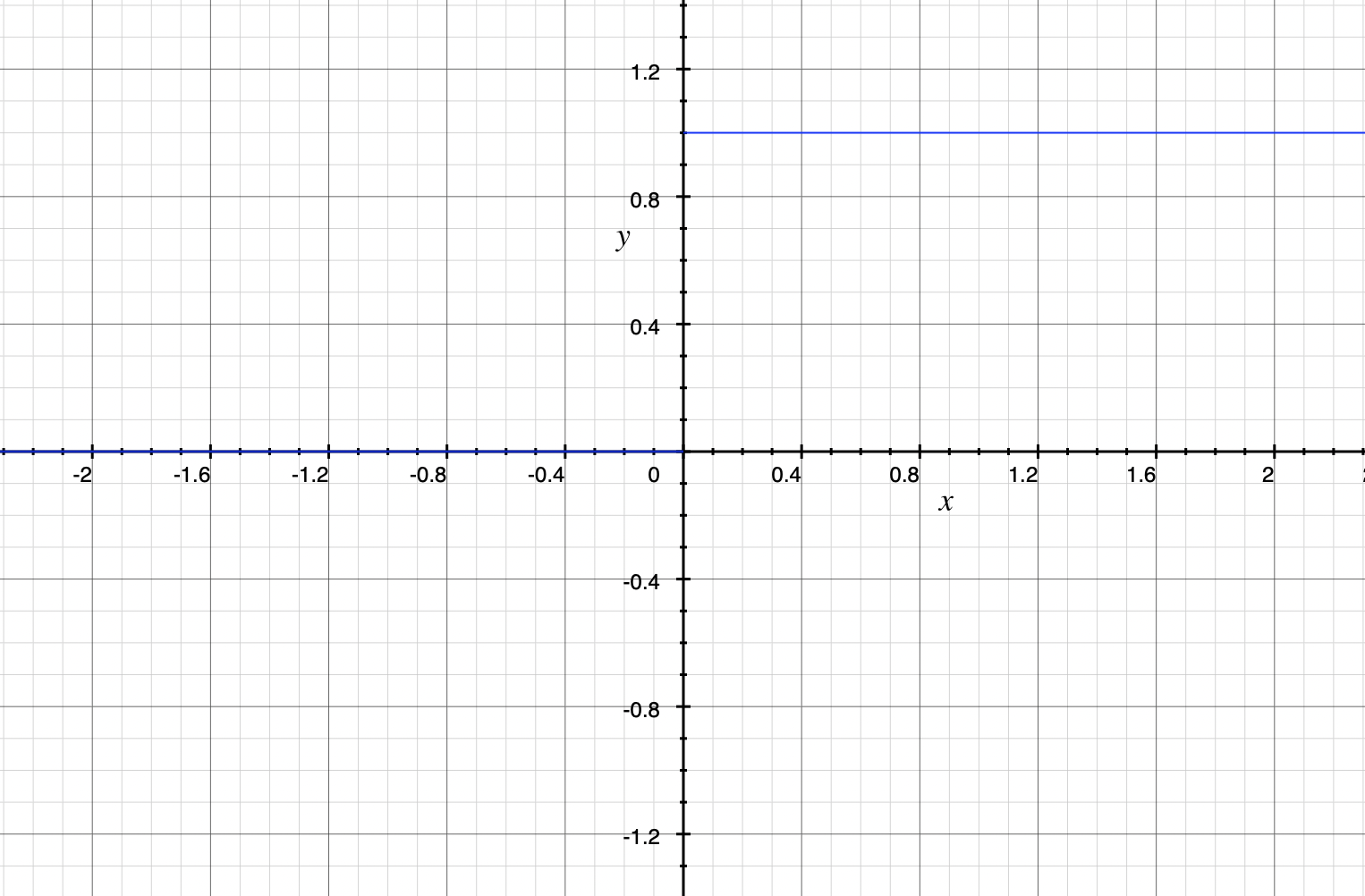
Python代码实现
import numpy as np
def relu(Z):
""" relu函数计算 """
return np.where(Z < 0, 0, Z)
def relu_derivative(Z):
""" relu函数导数计算 """
return np.where(Z < 0, 0, 1)
LeakyReLU
介绍
带泄露线性整流函数(Leaky Rectified Linear Unit, LeakyReLU), 在输入值 为负的时候,带泄露线性整流函数(Leaky ReLU)的梯度为一个常数 ,而不是0。在输入值为正的时候,带泄露线性整流函数和普通斜坡函数保持一致。
公式
$$ f(x)=\begin{cases} \alpha x \quad x< 0 \\ x \quad x\ge0\end{cases} $$
导数
$$ f'(x)=\begin{cases} \alpha \quad x< 0 \\ 1 \quad x>0\end{cases} $$
图像
说明
$ 以下图像中\alpha = 0.01 $
leaky relu 函数
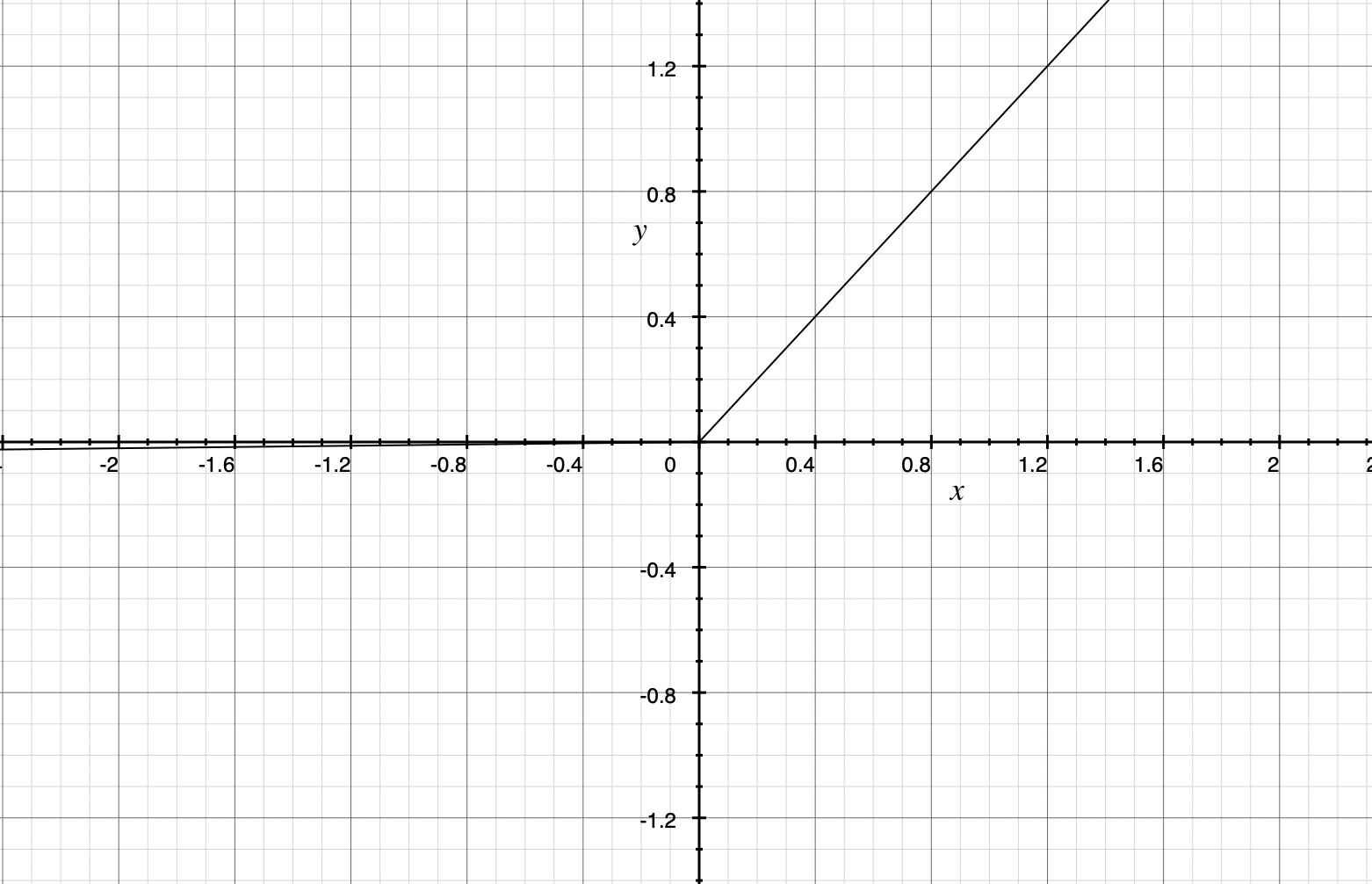
leaky relu 函数导数
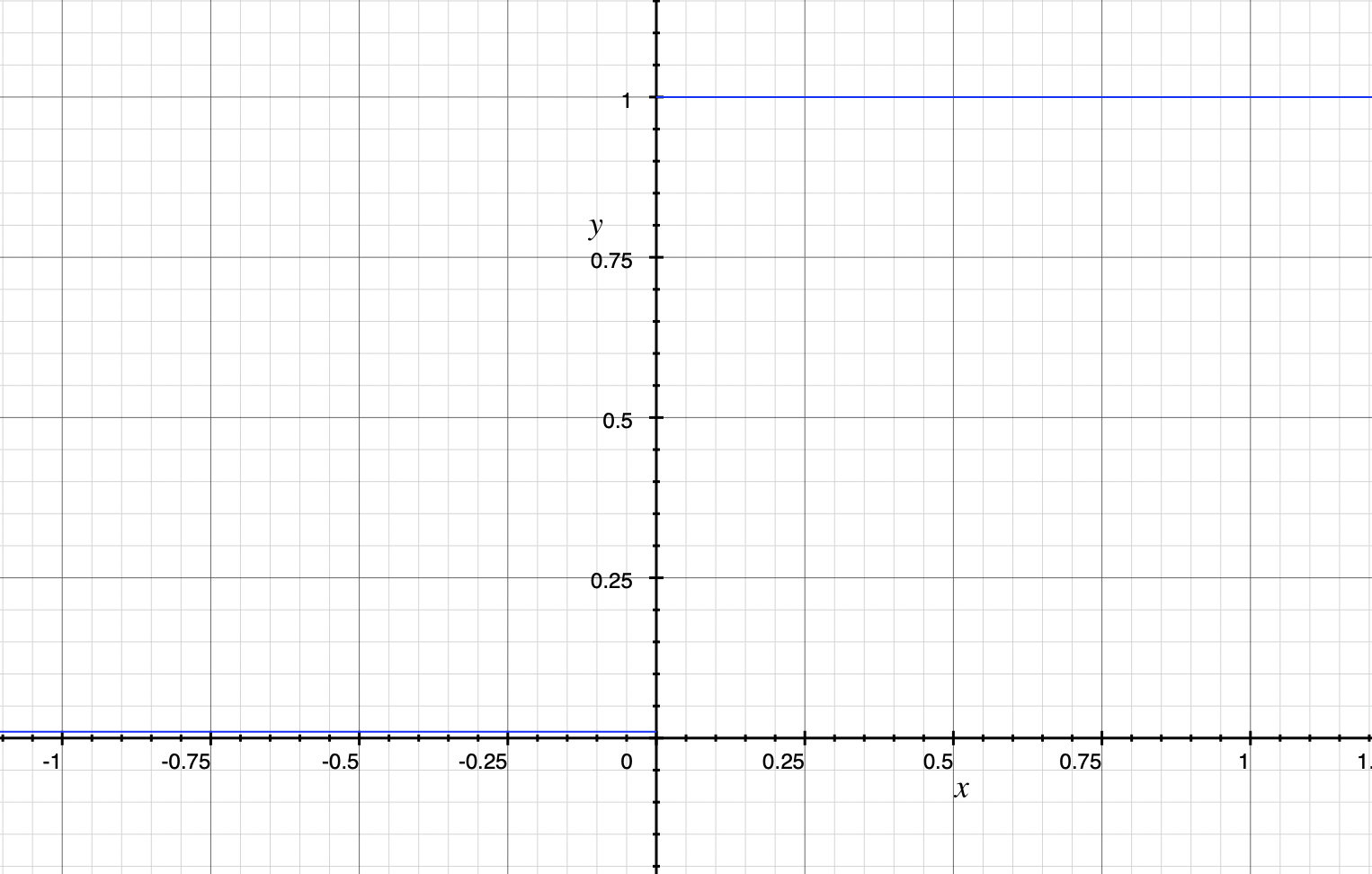
Python代码实现
import numpy as np
def leaky_relu(Z, a):
""" leaky relu 函数计算"""
return np.where(Z < 0, a, Z)
def leaky_relu_derivative(Z, a):
""" leaky relu 函数导数计算 """
return np.where(Z < 0, a, 1)
ELU
介绍
指数线性单元(Exponential Linear Unit, ELU),该激活函数由Djork等人提出,被证实有较高的噪声鲁棒性,同时能够使得使得神经元的平均激活均值趋近为 0,同时对噪声更具有鲁棒性,由于需要计算指数,计算量较大。
公式
$$ f(x)=\begin{cases} \alpha(e^{x}-1) \quad x< 0 \\ x \quad x\ge0\end{cases} $$
导数
$$ f'(x)=\begin{cases} \alpha e^{x} \quad x< 0 \\ 1 \quad x> 0\end{cases} $$
图像
说明
$ 以下图像中\alpha=1 $
ELU函数
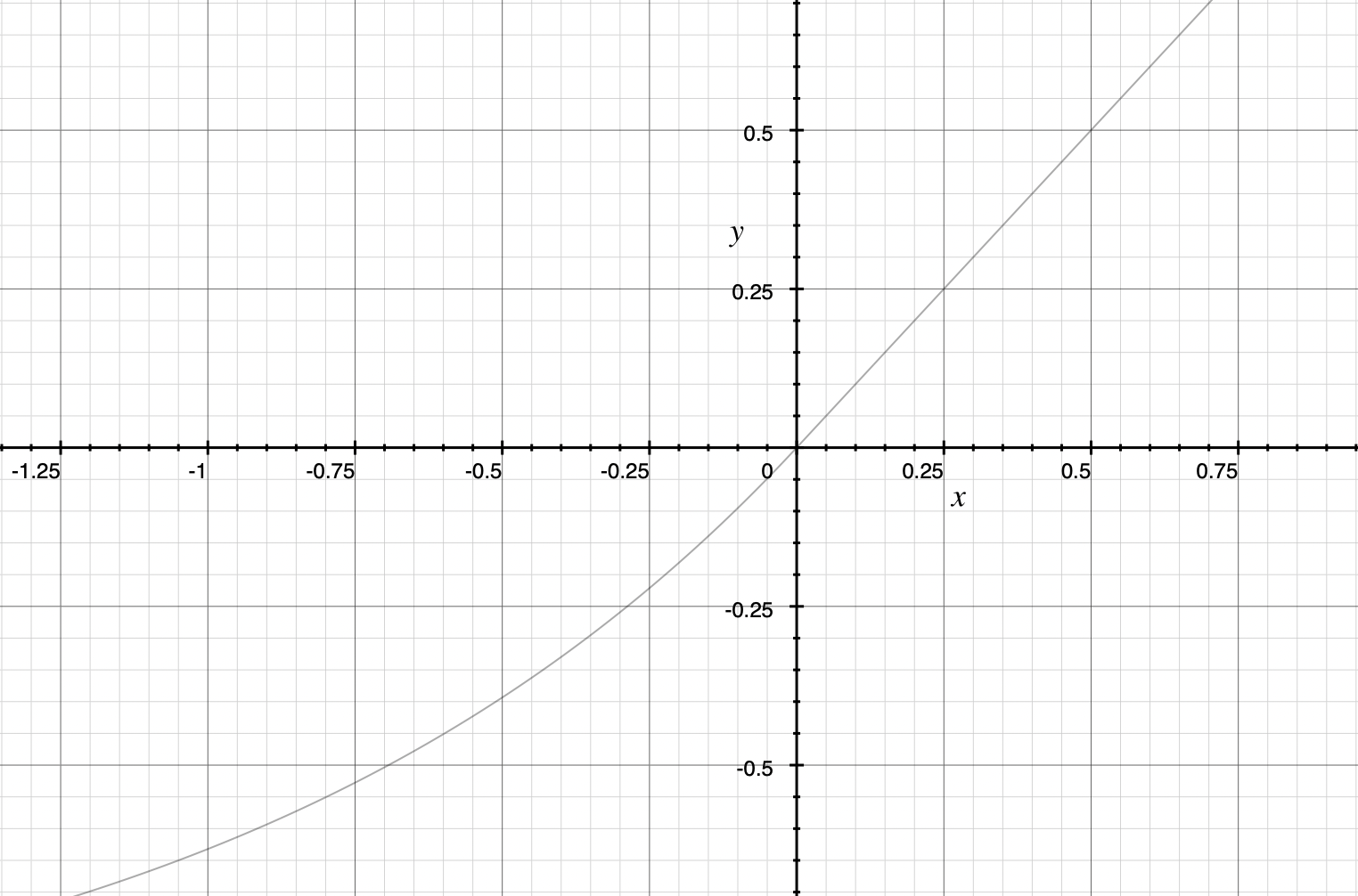
ELU函数导数
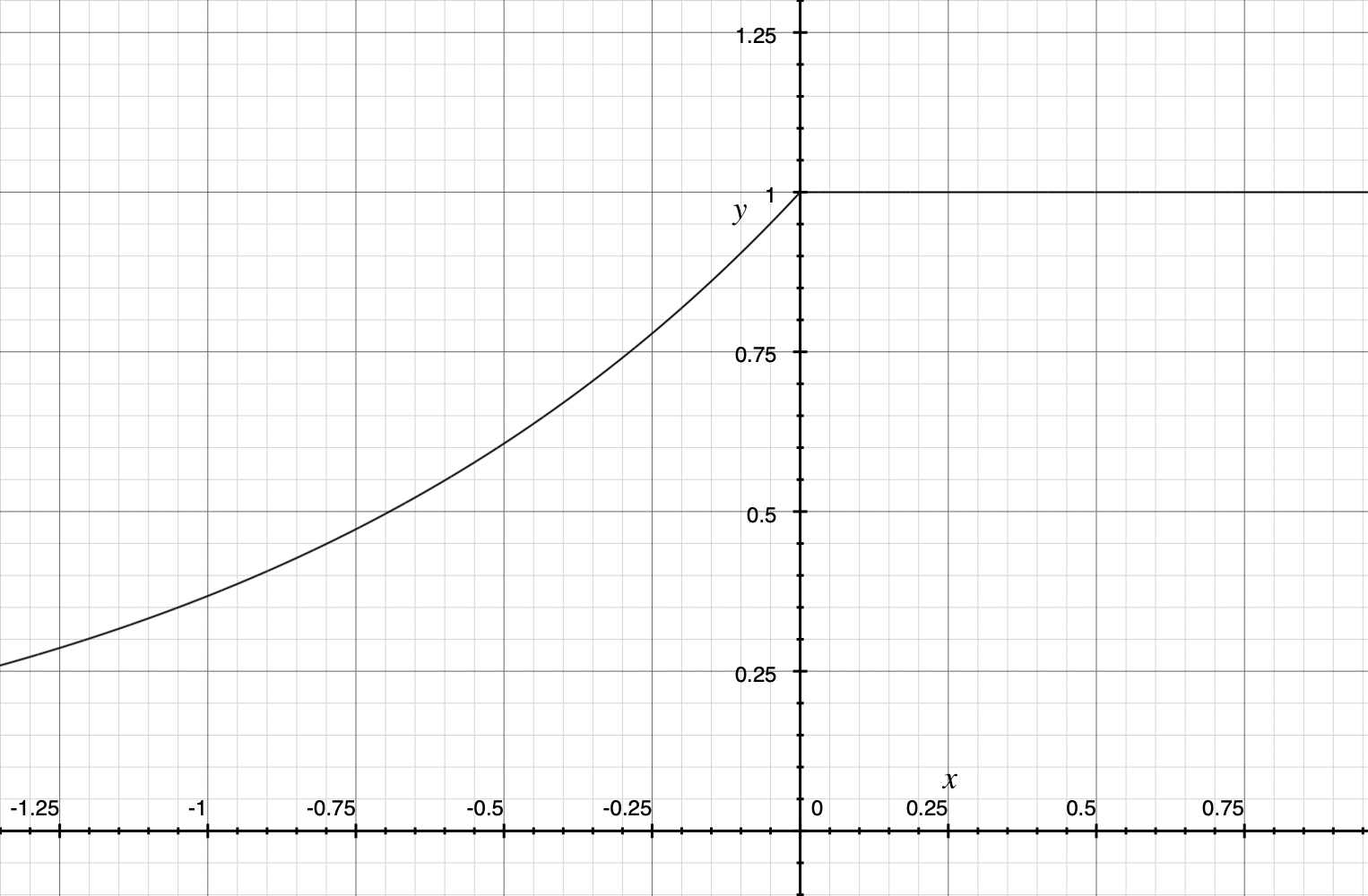
Python代码实现
import numpy as np
def elu(Z, a):
""" ELU函数计算 """
return np.where(Z<0, a*(np.exp(Z)-1), Z)
def elu_derivative(Z, a):
""" ELU函数导数计算 """
return np.where(Z<0, a*np.exp(Z), 1)
SoftPlus
介绍
公式
$$ f(x)=log(1+e^x) $$
导数
$$ f'(x)=\frac{1}{1+e^{-x}} $$
图像
SoftPlus函数
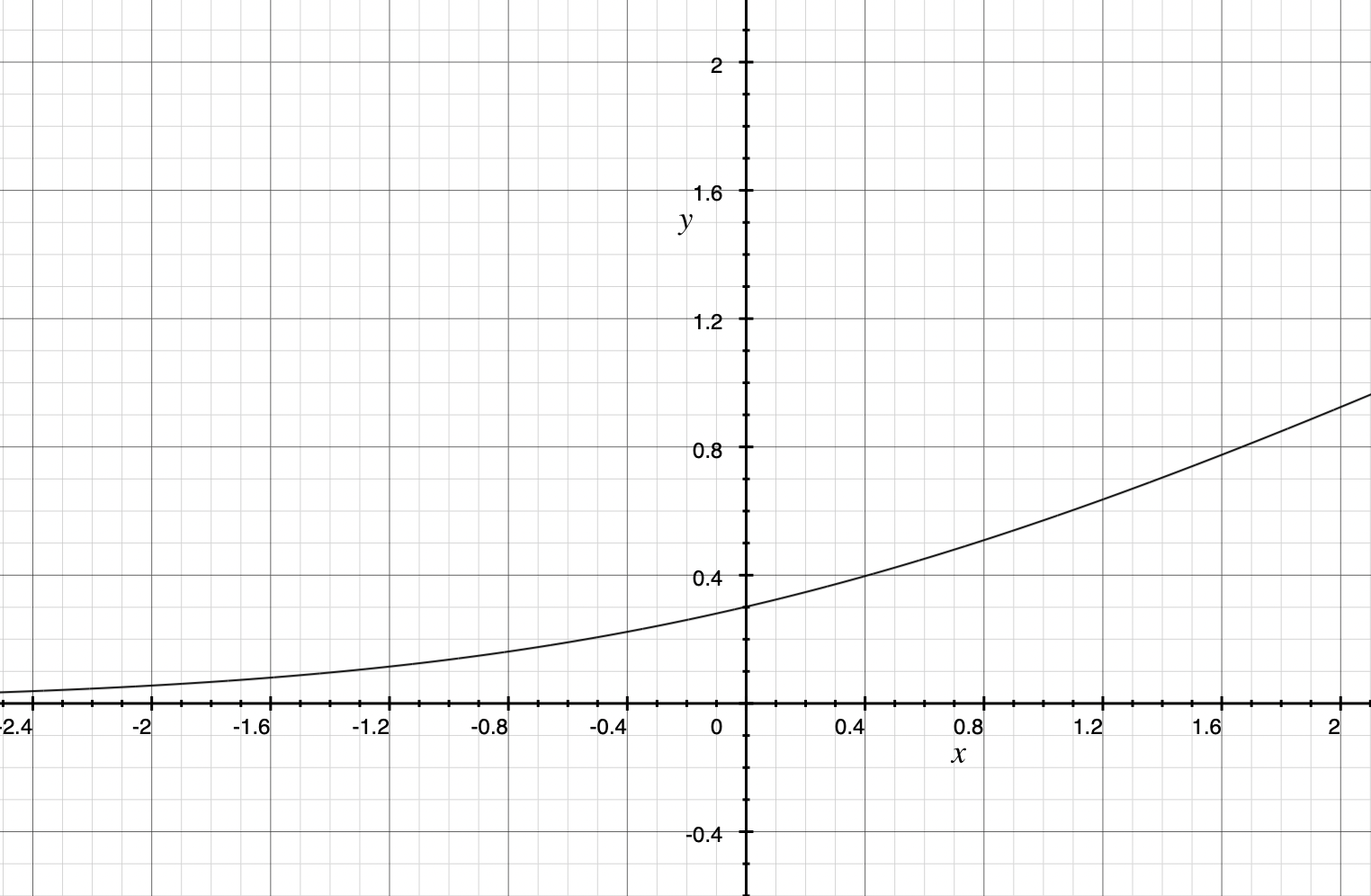
SoftPlus函数导数
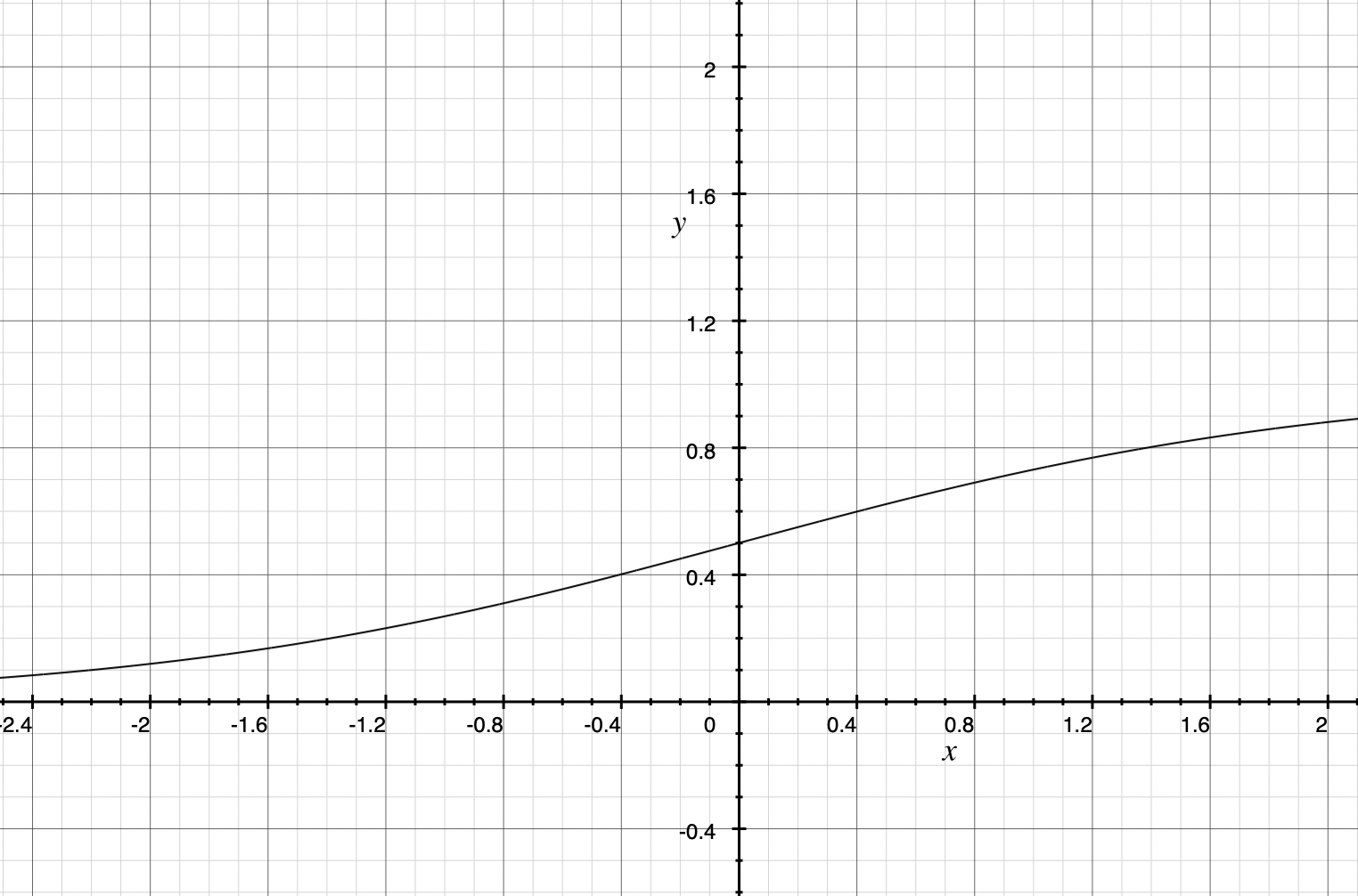
Python代码实现
import numpy as np
def softplus(Z):
""" SoftPlus函数计算 """
return np.log(1+np.exp(Z))
def softplus_derivative(Z):
""" SoftPlus函数导数计算"""
return 1/(1+np.exp(-Z))
Softmax
介绍
在数学,尤其是概率论和相关领域中,归一化指数函数,或称Softmax函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。该函数多于多分类问题中。